L'étude théorique du repérage isostatique
Les objectifs
Déterminer les surfaces d'appui sur la pièce à usiner, dans le but :
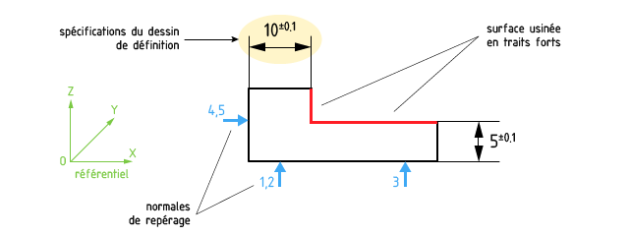
de respecter les spécifications du dessin de définition (DD),
de tenir compte de la répétitivité de l'usinage, dans un travail de série.
Le problème posé sera donc de repérer un solide dans un référentiel.
La détermination du référentiel
Un solide doit être situé dans un référentiel par un certain nombre de contacts ponctuels, qui représentent des liaisons.
Le référentiel est constitue par l'ensemble des objets mécaniques permettant d'assurer la mise en place correcte de la pièce pour un usinage déterminé. On utilise les axes normalisés des machines - outils (MO) :
Axe
axe de la broche principale,Axe
axe perpendiculaire à
et ayant le plus grand déplacement,Axe
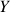
axe formant un trièdre de sens direct avec
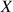et
.
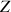Les degrés de liberté ; principe de Kelvin
Un solide libre dans l'espace (cas d'une pièce à usiner avant sa mise en position sur une machine) possède 6 degrés de liberté, que l'on défini ainsi, par rapport à un système d'axes orthogonaux :
3 Translations :
,
,
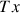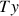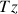
3 Rotations :
,
,
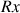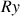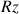
Les conditions d'isostaticité ; liaison de mise en position
En usinage, tout solide doit être assujetti à rester en contact avec un solide voisin (liaison). On caractérise la liaison entre le solide (pièce) S et le solide voisin S' (support de pièce) par la normale au contact
. Un solide parfait est repéré dans l'espace par six normales en six points distincts.
Pour assurer un repérage isostatique :
six normales sont nécessaires et suffisantes,
on pourra, au plus, trouver trois normales parallèles,
on pourra, au plus, trouver trois normales coplanaires.
En conséquence :
les six normales seront relatives à trois plans au maximum,
on pourra, au plus, trouver trois normales parallèles,
on pourra, au plus, trouver trois normales coplanaires.
Soit un point géométrique
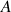, fixe par rapport au référentiel et en contact avec la surface BCDE du solide S. Celui-ci ne possède plus que 5 degrés de liberté :
,
,
,
,
(
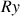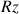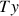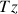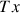supprimé). Le point géométrique
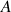sera appelé degré de liaison.
Conclusion : pour supprimer 6 degrés de liberté, il faut établir 6 degrés de liaison.
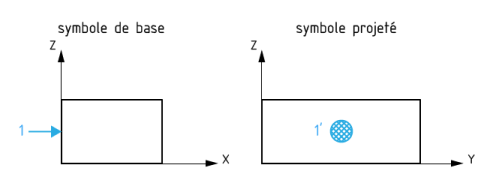
La représentation normalisée d'un degré de liaison
Le symbole de base est représenté ci-après. Il est noirci pour une meilleure visualisation. La projection éventuelle du symbole est un cercle avec hachures quadrillées. Ce symbole est placé sur la surface spécifiée ou sur une ligne d'attache, du côté libre de matière. Ce symbole est également normal à la surface.
Remarque :
Il s'agit, à ce niveau, d'un modèle géométrique (purement mathématique) qu'il faudra ensuite matérialiser par une symbolisation technologique qui sera présentée ultérieurement.
