Le transfert de cotes : cas des tolérances géométriques
Les transferts géométriques concernent des transferts faisant intervenir des tolérances géométriques de position. La méthode générale est la même que pour le transfert de cotes.
Remarque :
La résolution se présente sous deux formes générales :
l'une valable pour des tolérances de position (localisation, coaxialité et symétrie),
l'autre convenant aux tolérances d'orientation (inclinaison : parallélisme et perpendicularité).
A. Le transfert d'une coaxialité
a) Détermination d'une cote de brut
La cote
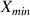sert notamment au calcul de la cote du brut.
Selon la chaîne de cotes (figure) nous pouvons écrire les relations suivantes :
b) Détermination d'une coaxialité
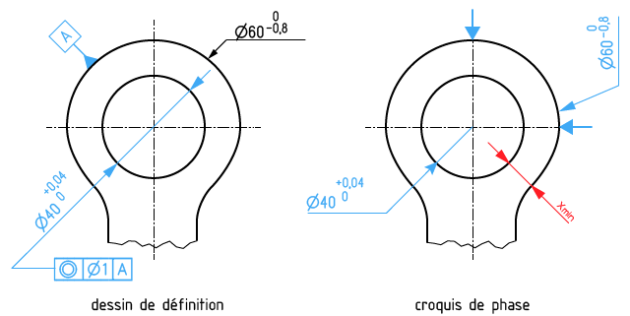
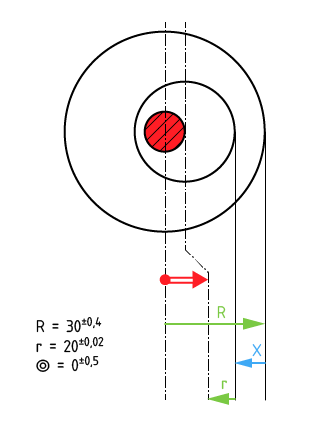
On impose une épaisseur minimale de matière Emin (condition de résistance) sur la pièce illustrée ci-après. Soit à calculer la tolérance de coaxialité qui permettra de respecter cette condition sachant que la mise en position axiale est réalisée par un vé à 90°.
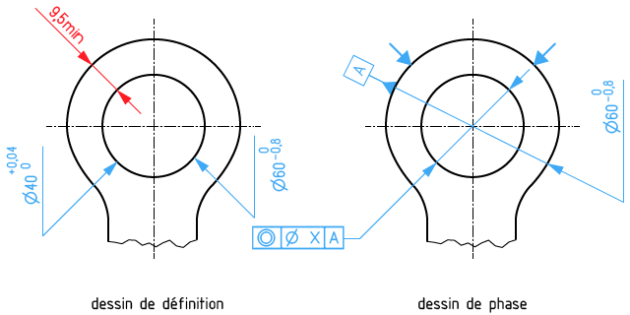
La chaîne de cotes permets de déduire les relations suivantes et de calculer la coaxialité maximale Xmax est la suivante:
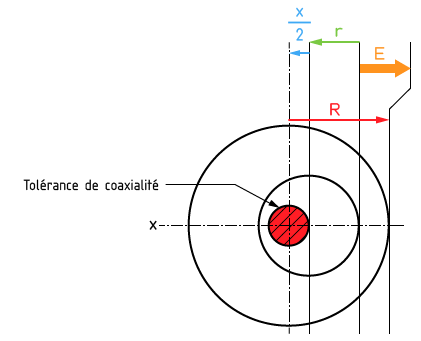
Emin = Rmin - (rmax + X/2max)
9,5 = 29,6 - (20,02 + X/2max)
X/2max = 29,6 - (20,02 + 9,5)
X/2max = 0,08
Xmax = 0,16
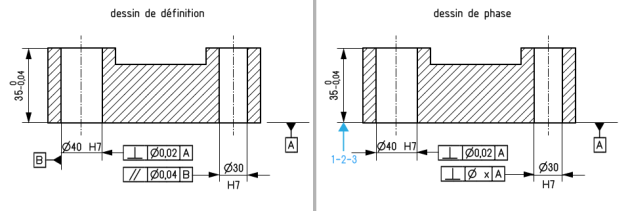
B. Le transfert d'une localisation
Le dessin de phase (figure ci-après) montre que le procédé de fabrication donne, pour l'axe de l'alésage, une zone de tolérance parallélépipédique à section carrée de côté t'. Cette zone de tolérance doit rester inscrite à l'intérieur du cylindre Φ t imposé par le dessin de définition (voir le détail de la zone de tolérance).
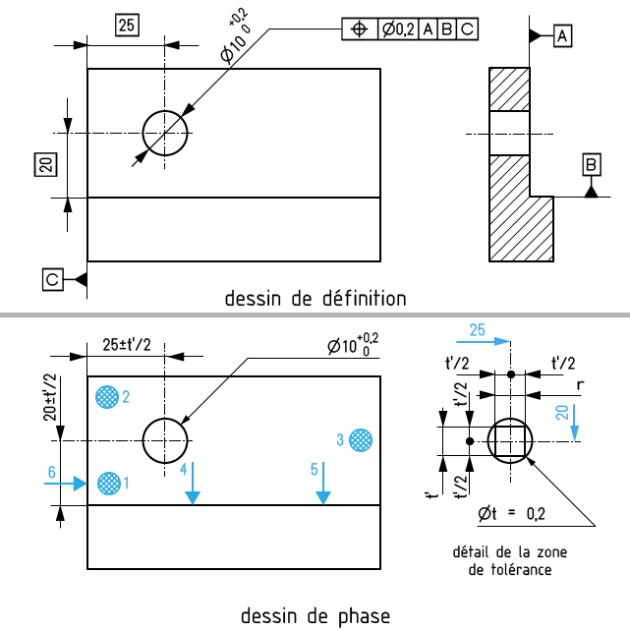
Soit :
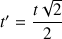d'où
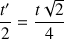
On déduit alors, à partir de cette relation :
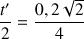
donc
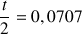
C. Le transfert d'une symétrie
Le dessin de phase montre que la position de la rainure est donnée par la cote X au lieu de la tolérance de symétrie. La cote condition est la tolérance de symétrie t = 0,08. On peut écrire également la cote condition :
t = ± 0,04.
Les cotes et les tolérances intervenant dans la chaîne sont les demi-cotes affectées de la demi-tolérance.
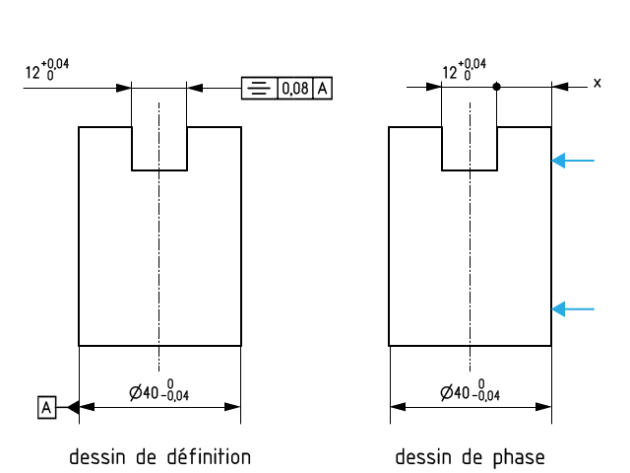
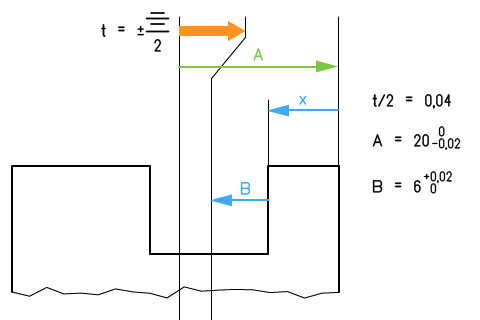
D'après la chaîne de cotes on a :
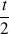max = Amax - (Xmin + Bmin)
0,04 = 20 - (Xmin + 6)
Xmin = 13,96
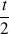min = Amin - (Xmax + Bmax)
-0,04 = 19,98 - (Xmax + 6,02)
Xmax = 14
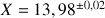
D. Le transfert d'une inclinaison
Le dessin de phase montre que la face inclinée est usinée en ayant la pièce en appui plan sur la face horizontale. L'angle obtenu est X.
Le calcul de la valeur X tolérée est réalisé en plusieurs étapes :
a) Écrire la tolérance de perpendicularité en valeur angulaire :
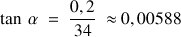
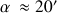
b) Choisir un système d'axes.
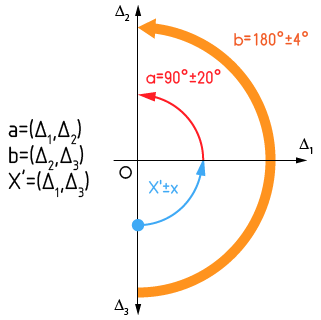
A partir d'un point O quelconque, tracer trois axes parallèles aux cotes des angles a, b et x. Le sens de chaque axe est indifférent.
c) Tracer la chaine de cotes angulaires.
Cette chaîne est constituée d'arcs de cercles orientés.
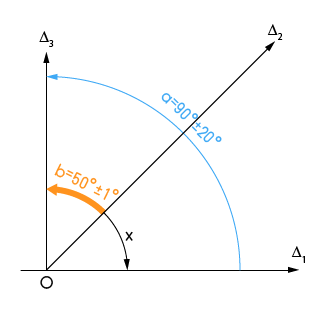
On applique à la chaîne la règle générale du transfert de cotes. Soit :
bmax = amax - Xmin
51° = 90°20' - Xmin
Xmin = 39°20'
bmin = amin - Xmax
49° = 89°40' - Xmax
Xmax = 40°40'
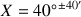
Vérification :
IT b = IT a + IT X donc, en valeurs numériques : ± 1° = (±20') + (±40')
Remarque :
Cette méthode s'applique si les axes
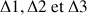sont coplanaires. Si l'inclinaison à transférer est oblique par rapport au plan de projection, on effectue deux transferts par rapport à deux plans de projection.
E. Le transfert d'un parallélisme
Le dessin de phase montre que les alésages
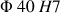et
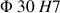sont usinés, la pièce étant en appui plan sur la surface A. On obtient, pour l'alésage
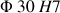, une perpendicularité par rapport à la surface A au lieu du parallélisme demandé entre les axes.
Le calcul de la valeur X tolérée sera réalisé en plusieurs étapes :
a) Ecrire les tolérances de perpendicularité et de parallélisme en valeurs angulaires :
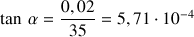
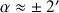
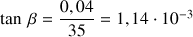
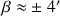
b) Choisir un système d'axes (comme précédemment). Pour une meilleure clarté on évite de prendre deux axes de même direction et de même sens.
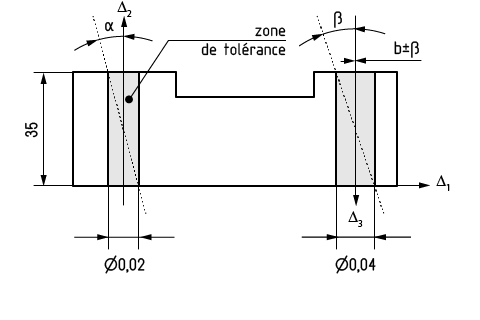
c) Tracer la chaîne de cotes. Cette chaîne est composée de cercles orientés. On peut appliquer la relation :
IT b = IT a + IT X donc, en valeurs numériques :
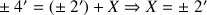
En convertissant cette tolérance angulaire en tolérance de perpendicularité :
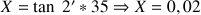
Remarque :
Dans le cas où la tolérance sur la cote transférée (cote condition) est inférieure à la somme des tolérances sur les cotes composantes, il est nécessaire de réduire les tolérances sur les cotes restantes.
